GEOPY

Métodos de Estadística Descriptiva Bivariante

La estadística descriptiva bivariante es el conjunto de técnicas estadísticas orientadas al análisis de dos variables aleatorias X, Y. Desde un punto de vista experimental hay situaciones en las que obtenemos los valores de X e Y en un mismo individuo o unidad de análisis. En tales casos el estudio estadístico descriptivo se realiza en cada variable por separado, pero además se estudia su posible relación estadística. La relación estadística o estocástica entre X e Y conduce a la existencia de una variable aleatoria bidimensional (X, Y) que recibe el nombre de variable aleatoria bivariante.

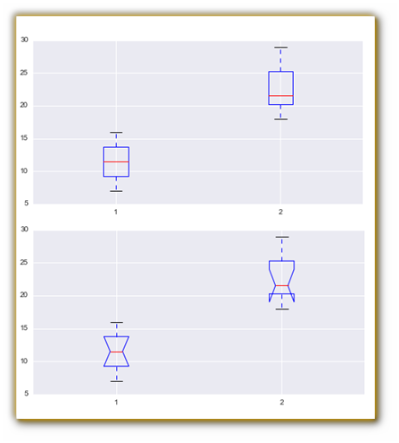
El estudio descriptivo de cada variable X e Y por aislado se resume a las medidas de centralización, dispersión y forma habituales. Sin embargo en estadística descriptiva bivariante no es frecuente calcular como en el caso univariante muchas de las medidas disponibles, obteniéndose principalmente la media aritmética, varianza y desviación típica. Los métodos gráficos son los mismos de la estadística descriptiva univariante, por ejemplo se suele representar dos gráficos de caja y bigotes de los datos experimentales X e Y.

• Explicación del script
  

Entre las líneas 28 y 42 se realiza el estudio descriptivo de cada variable X e Y por separado obteniéndose las medidas de centralización, dispersión y forma habituales. En el caso bivariante no se calculan como en el caso univariante todas las medidas disponibles. En el script se obtienen entre otras medidas, la media aritmética, varianza y desviación típica.

Los métodos gráficos son los mismos de la estadística descriptiva univariante. Entre las líneas 54-59 se muestra el script que permite con la orden:

plt.boxplot([col1,col2],_,' ')

representar dos gráficos de caja y bigotes de los datos experimentales X e Y.

[ver código en Python]

En el script se incluyen los tres análisis estadísticos que son característicos del caso bivariante:

• Matriz de varianzas-covarianza (líneas 47-52).

• Matriz de correlación (líneas 43-46).

• Matriz de dispersión (líneas 61-64).

No obstante, en estadística descriptiva bivariante se realizan análisis adicionales con el fin de establecer si existe, y en tal caso en que grado, una relación lineal entre ambas variables.

En general, tres son los análisis estadísticos que son característicos del caso bivariante:

[Definiciones, conceptos y métodos]

Laboratorio
_____________________________________________________________________________________________________

• Estudio biométrico en una especie de arácnido fósil
  

En un estudio se mide en 200 arañas fósiles la longitud del tarso (X) y fémur (Y). Realizar un análisis de estadística descriptiva bivariante obteniendo la matriz de varianzas-covarianza, la matriz de correlación y el ajuste de los datos (estimación de los parámetros a y b) a la recta de regresión Y = a + b X:

• script: spider.py
  

• archivo de datos: spiders.dat  spiders.csv
  

Solución: ejemplo21.mp4

Un análisis de estadística descriptiva bivariante secompleta con el análisis de regresión lineal entre las variabes X e Y. Con tal fin se ilustra en en el script el empleo de distintas librerias de rutinas para Python:

• En primer lugar se recurre a statsmodels (líneas 66-71) proporcionando la información más completa sobre el ajuste. Sin embargo, con fines descriptivos es suficiente si se recurre a los dos siguientes métodos.

• En segundo lugar (método 1) se utiliza scipy (líneas 73-77) obteniéndose menos información que con la librería anterior, pero suficiente en un análisis de estadística descriptiva bivariante. Se obtiene la estimación de los parámetros a y b, y el p-valor. También se obtiene en la línea 77 el diagrama o matriz de dispersión con la orden:

plt.scatter(col1, col2, alpha=0.3).

• En tercer lugar (método 2), utilizando numpy se realiza (línea 80) con la orden:

m, b = np.polyfit(col1, col2, deg=1)

se obtiene la representación de la recta de regresión, tal y como se ilustra con el código entre líneas 79 y 88.