GEOPY
Menu Principal
MEDU
Estadística
Descriptiva Univariante
La estadística descriptiva es un conjunto de
técnicas estadísticas que permiten obtener una
primera impresión de la información contenida en
los datos. Su finalidad es sintetizar o resumir la
información de la muestra (conjunto de datos u
observaciones), organizar los datos en tablas y representarlos
gráficamente. De esta forma el investigador, a partir de los
datos obtenidos en un primer experimento piloto, cuenta con
herramientas estadísticas que le permitirán
formular hipótesis o conjeturas acerca del
fenómeno objeto de estudio.
La estadística descriptiva puede aplicarse al
análisis de una variable aleatoria X o dos variables
aleatorias X e Y, refiriéndonos a uno y otro de
los casos como estadística descriptiva univariante y
estadística descriptiva bivariante.
-
Preliminares
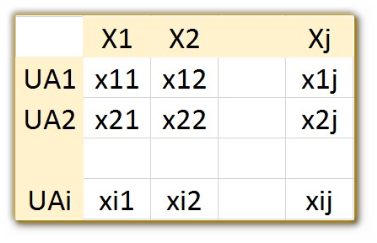
En primer lugar organizaremos los datos experimentales en una tabla de
datos. Se trata de una matriz 2x2 con el siguiente formato: en filas se
ubican los elementos o sujetos que son objeto de estudio, llamados
unidades de análisis:
(UA1,
UA2, …, UAi)
y en columnas los valores de las variables aleatorias:
(X1,
X2,…, Xj)
Por consiguiente, un vector columna (j) es una muestra aleatoria,
mientras que un vector fila (i) es un vector de observaciones.
La estadística descriptiva resume la información
contenida en una muestra en tres clases de valores numéricos
a los que se denomina como medias de centralización,
dispersión y forma.
[ Definiciones,
conceptos y métodos]
-
Explicación del script
En las
líneas 33-
np.percentile(data,_)
Las medidas de dispersión son obtenidas a
continuación. Varianza, desviación
estándar, error estándar de la media, rango
intercuartílico y coeficiente devariación de
Pearson son calculados en las líneas 49-
Un variable
aleatoria es una
propiedad observable.
Si es cuantitiativa entonces puede ser continua, es decir se trata de
una propiedad medible; o discreta cuando la propiedad es contable.
Las variables
aleatorias se
clasifican según el siguiente criterio:
-
Cuantitativas:
-
-
-
Cualitativas:
-
-
-
Llamaremos
observaciones a los
valores de la variable X, que representaremos como una secuencia:
{x1,
x2, ... , xn}
Con el fin de simplificar la notación en esta secuencia nos
referimos con x1 al valor de la variable en la primera unidad de
análisis, x2 al valor en la segunda unidad de
análisis etc. El valor de n es el tamaño
muestral, es decir el número de elementos, objetos o
unidades de análisis en los que ha sido obtenido
experimentalmente el valor de la variable aleatoria X.
Laboratorio
Los
métodos
gráficos más habituales se realizan con el
fragmento de código representado en el script entre las
líneas 61-
Entre las líneas 79-
plt.hist(data,numBins,_,…,_)
La sección de código que sigue (líneas
85-
______________________________________________________________________________________________________________________________
-
Estudio de los niveles de ozono en una ciudad
En una determinada ciudad se
registran los niveles de ozono máximos durante 60
días. Sea X la variable aleatoria "nivel de ozono
máximo por día", efectúese el
correspondiente análisis estadístico descriptivo
de la variable objeto de estudio ¿Qué podemos
concluir?¿hay días con valores
atípicos o extremos de ozono?
Solución: ejemplo11.mp4
______________________________________________________________________________________________________________________________
-
Estudio de la cantidad de silicio en una roca sedimentaria
En un experimento de campo se estudia en una roca sedimentaria la
variable aleatoria X "cantidad de silicio por roca". Si realizamos un
análisis estadístico descriptivo de la variable
¿Qué anomalía hemos detectado en este
estudio? ¿cómo se distribuye el silicio en esta
roca sedimentaria?
-
script: Silicon.py
-
archivo de datos: Silicon.dat
Solución:
ejemplo12.mp4