GEOPY

Métodos de Inferencia Estadística con Proporciones y Frecuencias

Hay circunstancias experimentales en las que el tratamiento cuantitativo del estudio requiere del uso de proporciones. De hecho son numerosas las áreas de conocimiento en las que los análisis estadísticos con proporciones son tan comunes como los test basados en el uso de medias y varianzas.

Más aún, son también frecuentes los experimentos en los que los datos son organizados en tablas de contingencia. Se trata de tablas RxC (rows x columns en inglés) en cuyas entradas para las filas y columnas se recogen los valores de dos variables cualitativas, ya sean nominales (por ejemplo, sexo, grupo sanguíneo, pH, clase de roca etc.) u ordinales (por ejemplo, escala de Mohs, color del vino etc.). En las celdas de la tabla se anotan las frecuencias absolutas, es decir el número de observaciones o unidades de análisis que verifican simultáneamente dos valores dados de las variables cualitativas.

• Test de proporciones
  

A continuación describimos las pruebas o test estadísticos específicos para el análisis de proporciones en una y dos poblaciones o grupos experimentales:

[ Definiciones, conceptos y métodos]

• Test de chi-cuadrado
  

El análisis de tablas de contigencia o tablas RxC por medio del test de chi-cuadrado o ji-cuadrado es descrito a continuación:

[  Definiciones, conceptos y métodos]

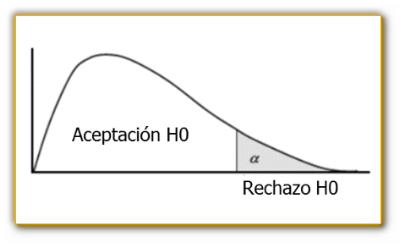
Esta prueba, una de las más útiles y populares en estadística, se caracteriza porque el contraste de hipótesis no es sobre el valor de un parámetro estadístico sino sobre una afirmación estadística. En este caso es interesante observar que la región de significación, es decir de rechazo de la hipótesis nula H0, se encuentra a la derecha de la distribución chi-cuadrado; estando la región de aceptación ubicada entre 0 y el valor crítico en la distribución. No obstante, en la práctica se calcula el p-valor rechazándose la H0 si dicho valor es menor al nivel de significación elegido, por ejemplo 0.05.

En la línea 17 llamamos a la libreria statsmodels.stats.proportion realizándose el test de una proporción con la orden de la línea 25:

z,p = proportions_ztest(x, n, H0, HA)

cuyo resultado se muestra en línea 27.


De forma similar, entre las líneas 30 y 43 se muestra el código que permite realizar un test de dos proporciones. Se trata de una prueba paramétrica que requiere que las dos muestras sean de tamaño grande (n1, n2 > 30). En el ejemplo (líneas 31-34) disponemos de dos muestras de igual tamaño muestral. En la primera muestra 702 individuos presentan una determinada característica entre un total de 1000 individuos, y en la segunda muestra el número de individuos que presenta dicha características es de 198 entre 1000 individuos. Las muestras pueden ser de igual o diferente tamaño siempre y cuando ambas sean muestras grandes. El ejemplo asume en la H0 la igualdad de proporciones, es decir H0: P1=P2 o de forma equivalente H0: P1-P2=0. Puesto que las proporciones muestrales son muy diferentes, p1=702/100 y p2=198/100, esto es 0.70 y 0.19, nos preguntaremos si esta diferencia es o no significativa estableciendo un contraste de hipótesis bilateral. Por consiguiente la hipótesis alternativa será Ha: P1-P2 distinta de cero (línea 37). Entre las líneas 38 y 40 se muestra el código que realiza el test de dos proporciones:

x12 = np.array([x1,x2])
n12 = np.array([n1, n2])
z,p = proportions_ztest(x12, n12, H0, HA)

Finalmente, en la línea 42 se muestran los resultados obtenidos en la prueba estadística.

[ver código en Python]

•  Tablas de contigencia y tes de chi-cuadrado
  

Entre las líneas 45 y 74 se muestra el código en Python para un test de chi-cuadrado para el caso de una tabla de contigencia 2x2. En la línea 48 definimos la tabla de contingencia a la que damos un nombre arbitrario, por ejemplo data_observed, siendo los elementos de la tabla los datos experimentales, esto es las frecuencias observadas.
En la línea 49 usamos la orden:

chi2_contingency(data_observed)

• Explicación del script
  

• Test de proporciones
  

Entre las líneas 19 y 28 se muestra con un ejemplo el código que permite realizar el test de una proporción. Se trata de una prueba paramétrica en la que ha de cumplirse que el tamaño muestral es grande (n>30). En el ejemplo se define una variable binomial X en una muestra de 96 indivíduos (línea 21), siendo X "el número de individuos que presentan una cierta característica". Experimentalmente se obtiene el valor de X, siendo igual a 69 (línea 20). Si calculamos en la muestra la proporción p, es decir x/n y por tanto 69/96 en el ejemplo, obtendremos 0.71, valor que es inferior al que es propuesto en la hipótesis nula H0: P=0.8 (línea 22). En la línea 24 especificamos la hipótesis alternativa, siendo en el ejemplo Ha: P < 0.8. Esta hipótesis se declara eligiendo según el caso alguna de las palabras reservadas que se muestran en la línea 23.

de la librería  scipy.stats (línea 15). A continuación, especificamos el nivel de confianza, por ejemplo el 95%, tal y como se muestra en la línea 51: confidence_level = 0.95.
El test exacto de Fisher (línea 54) permite averiguar si dos variables dicotómicas están o no asociadas, mostrándose en una tabla de resultados el test de chi-cuadrado y test exacto de Fisher (líneas 55-74). Al final de la tabla de muestran las frecuencias observadas y esperadas (líneas 68-71), mientras que al principio de la tabla se recogen los valores del estadístico chi-cuadrado (línea 57), p-valor (línea 58) y grados de libertad (línea 59). También se muestra el valor crítico de la distribución chi-cuadrado (línea 60), valor que ha sido obtenido con la orden de la línea 52 perteneciente a la librería  scipy.stats (línea 15):

chi2.ppf(q = confidence_level, df=df_value)

Entre las líneas 76 y 97 se muestra un ejemplo de test de independencia. La prueba es similar a la anterior, excepto que no se realiza el test exacto de Fisher ya que las variables no son dicotómicas.

Laboratorio

______________________________________________________________________________________________________

• Análisis granulométrico del suelo ¿es el suelo apto para la agricultura?
  

En un terreno se obtiene una muestra de tierra, realizándose un análisis de su granulometría. El resultado del análisis fue que de un total de 42 fracciones de tierra 15 son arenas, el suelo ¿es apto para el cultivo? ¿Qué supuesto debe verificarse para poder utilizar este estadístico? ¿Qué distribución tiene la variable “proporción muestral”?

Utilizar la siguiente tabla. Identificación del tipo de suelo según su granulometría:

Tabla.- Clases de suelo

__________________________________________________________________________________________________________
Arcilloso: 25% de arenas, 75% limo y arcillas. Muy porosos, poca aireación. Retienen mucha agua. No son aptos para la agricultura.

Arenoso: 75% de arenas, 25% limo y arcillas. Gran aireación, no retienen agua. No son aptos para la agricultura.

Francos: 45% de arenas, 55% limo y arcillas. Texturas media. Si son aptos para la agricultura.

__________________________________________________________________________________________________________

• script: Soil.py
  

Solución: ejemplo51.mp4

_____________________________________________________________________________________

• Incidencia del cáncer en un pueblo de la provincia de Orellana (Ecuador)
  

En un estudio realizado en un pueblo de la provincia de Orellana (Ecuador) se obtuvieron los porcentajes de enfermos de cáncer (E) y personas sanas (S) en dos ubicaciones distintas tomando como referencia la presencia de un pozo de petróleo. En las personas allí residentes que bebían agua obtenida de una fuente a menos de 50 m del pozo de petróleo, el porcentaje de personas S y E era igual al 43% y 57% respectivamente. Por el contrario, en los sujetos que bebían agua de una fuente situada a más de 250 m del pozo de petróleo, el porcentaje de personas S y E era del 94.3% y 5.7% respectivamente ¿Qué podemos concluir?

• script: cancer.py
  

Solución: ejemplo52.mp4