GEOPY
Menu Principal
METGLREGRELIN
Modelos
Generales Lineales: REGRESIÓN LINEAL
El
análisis de regresión lineal tiene por finalidad la
modelización de la asociación estocástica, en el
caso más sencillo, entre dos variables aleatorias: una variable
Y o variable respuesta (la variable dependiente) y una variable X o
variable predictora (variable independiente). Si dicha relación
existe, deberemos estimar el grado de asociación lineal entre
variables, conociéndose a esta clase de análisis con el
nombre de análisis de correlación.
De forma análoga al ANOVA, a continuación definiremos
algunos de los términos más usuales en esta clase de
análisis estadístico:
• Variable dependiente o respuesta (Y): es la variable aleatoria
con distribución normal que no está controlada
experimentalmente y cuyo valor se desea predecir. Por ejemplo, en un
grillo la temperatura ambiental (Y) y el número de cantos o "cri-
En el análisis de regresión la variable dependiente Y es
equivalente en el ANOVA a la variable X o respuesta cuya varianza es
descompuesta en sus componentes o fuentes de variación.
• Variable independiente o predictora (X): es la variable no
necesariamente aleatoria, controlada experimentalmente, y a partir de
cuyo valor se desea predecir el valor de la variable Y.
En el análisis de regresión lineal las variables
independientes son equivalentes a los factores de un ANOVA.
• Ecuación de regresión o ecuación del
modelo: es la función, en el caso más sencillo de una
única variable independiente X, que relaciona a la variable Y
con X:
y = a +
b x
Lo coeficientes o parámetros de la ecuación son a (origen
en ordenadas o punto de corte en Y) y b (pendiente), siendo
estimados a partir de los valores experimentales (X, Y).
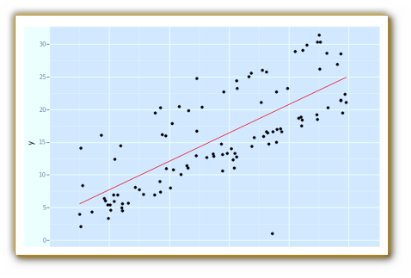
• Nube de puntos: es la figura que resulta de representar
gráficamente los puntos (Xi, Yi) cuyas coordenadas son los
valores experimentales de X e Y medidos en el individuo i.
También recibe el nombre de diagrama de dispersión.
-
Contraste de hipótesis con los parámetros de la recta de regresión
En un análisis de estadística descriptiva bivariante la
regresión lineal tiene por finalidad el estudio de una posible
asociación lineal entre las variables X e Y. En tal caso, con la
estimación de los parámetros a y b es
suficiente. Sin embargo, cuando la finalidad es establecer un modelo
que nos permita predecir el valor de la variable Y en función de
X, entonces estaremos en un contexto inferencial que precisa de la
realización de contrastes de hipótesis acerca de los
parámetros de la ecuación de regresión, es decir
tanto de la ordenada en el origen como de la pendiente. A
continuación, se explican estos contrastes:
[ Definiciones,
conceptos y métodos]
-
Explicación del script
Antes de
tratar el modelo de regresión lineal simple, el código
(líneas 28-
Si el modelo de regresión lineal es aplicado con fines descriptivos
(Método 1: líneas 104-
scipy.stats
as s
obteniendo el output llamando a la orden (línea 105):
slope_result,
intercept_result, r_value, p_value,
std_err_result=s.linregress(col1,col2)
En el output obtenemos la estimación de los
parámetros a (intercept) y b (slope) así
como el coeficiente de correlación de Pearson y el p-
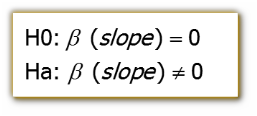
El
análisis de regresión lineal puede ser aplicado bajo dos
propósitos o enfoques diferentes, ya sea con una finalidad descriptiva
o con un enfoque inferencial:
-
Enfoque descriptivo: la regresión lineal es una técnica que se incluye como una prueba más junto con otros métodos de estadística descriptiva bivariante (matriz de varianzas-
covarianza, matriz de correlación y matriz de dispersión). El objetivo es estudiar la posible asociación lineal entre dos variables aleatorias X e Y.
-
Enfoque inferencial: la regresión lineal es la técnica principal de modelado, siendo el objetivo final el establecimiento de un modelo de regresión que permita predecir el valor de la variable respuesta Y a partir de un valor dado de la variable predictora X. Se incluyen pruebas o test de contraste de hipótesis sobre los parámetros a y b de la recta de regresión y = a + b x.
A continuación, se explica cómo a partir de unos datos
experimentales se obtiene la ecuación de la recta de
regresión:
[ Definiciones, conceptos y métodos]
-
Introducción a los Modelos Generales Lineales
A continuación, se explica qué tienen en común los
modelos de regresión lineal y ANOVA:
Obviamente el modelo de regresión lineal y = a + b x será
válido si p-
Ahora bien, si el modelo de regresión lineal es aplicado con un
objetivo inferencial, es decir con la finalidad de disponer de un
modelo predictivo (Método 2: líneas 116-
statsmodels.api
as sm
En este caso realizamos inferencias acerca de los parámetros de
la ecuación de regresión lineal, obteniendo un output
con más información del modelo. Si se desea
información detallada de los test realizados con statsmodels se
recomienda la lectura de este sitio web de referencia.
Laboratorio
___________________________________________________________________________________
Absorción de fosfato en una planta
Supóngase que en un grupo formado por 9 plantas analizamos la
cantidad de fosfato X presente en la tierra de cada maceta (archivo
phosphate, columna izquierda) y la cantidad de fosfato Y asimilado por
la planta (archivo phosphate, columna derecha). Contruir un modelo de
regresión lineal entre X e Y.
script: Phosphate.py
archivo de datos: phosphate.dat
Solución: ejemplo61.mp4