GEOPY

Métodos de Inferencia Estadística con dos poblaciones

Una de la situaciones más frecuentes en inferencia estadística tiene lugar cuando se comparan dos grupos de individuos o grupos experimentales en cuyos individuos ha sido definida una variable aleatoria con distribución normal. Asumiremos que el grupo 1 es aquel cuyos individuos son sometidos a un tratamiento 1, mientras que el grupo 2 es el grupo control o grupo de individuos sin tratamiento; o el grupo 1 recibe un tratamiento 1 y el  grupo 2 un tratamiento 2. El tratamiento puede un medicamento, abono, aplicación de un compuesto químico etc.; o un factor biótico como la pertenencia a un grupo social, sexo, presencia de un gen; o cualquier factor abiótico como por ejemplo la ubicación geográfica, clima, temperatura etc. En esta clase de situación experimental el modelo estadístico asume que un tratamiento tendrá un efecto si aumenta o disminuye el valor medio de la variable en un grupo experimental, considerándose este aumento o disminución con respecto a la media del otro grupo experimental.

[ Definiciones, conceptos y métodos]

• Explicación del script
  

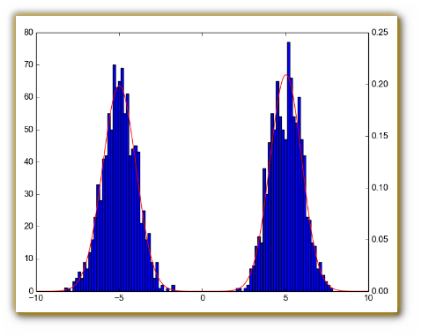
De forma similar a la inferencia estadística con una población, en la inferencia estadística con dos poblaciones un paso previo consiste en la realización de un análisis de estadística descriptiva con los datos experimentales de cada muestra (líneas 26 y 40), obteniéndose además distintas clases de gráficos que nos ayudarán en la interpretación de los resultados. En el script se muestra el código que permite obtener con los datos de las dos muestras su correspondiente diagrama de dispersión, gráfico de caja y bigotes, gráfico de probabilidad normal, histograma e histograma gaussiano (líneas 42-85).

Si efectivamente se cumple el supuesto de normalidad de la variable entonces se estará en condiciones de realizar el contraste de medias poblacionales aplicando pruebas paramétricas, por ejemplo el t-test (líneas 134-153). En tal caso, el script efectúa en primer lugar el F-test, contrastando la igualdad o no de las varianzas poblacionales (líneas 116-125). Además se muestra el código con el que también podemos efectuar una prueba de homogeneidad o igualdad de varianzas poblacionales, por medio de otras pruebas o test específicos: el test de Bartlett (líneas 126-128) y test de Levene (líneas 129-131).

[ ver código en Python]

El t-test para dos medias poblacionales (líneas 134-153) utiliza una misma función, pero se indica si las varianzas poblacionales son iguales escribiéndose la función por defecto (línea 136) :

s.ttest_ind(col1, col2)

o si son distintas, escribiéndose (línea 138):

s.ttest_ind(col1, col2, equal_var=False)

En la línea 143 se ha fijado un valor del nivel de significación del 5%, valor que debe ser cambiado en función del riesgo que conlleve aceptar la H0. Entre las líneas 140 y 153 se aplica la regla de decisión, en las dos situaciones con respecto a las varianzas poblacionales.

Finalmente, se muestra el código que realiza el test de la U de Mann Whitney (líneas 154-161). Se trata de la prueba no paramétrica a efectuar si no se cumpliera el suspuesto de normalidad de la variable, evaluándose en el contraste la igualdad de medianas poblacionales:

A continuación, entre las líneas 88 y 114 se efectúan los tests de normalidad con los datos de cada muestra: test de Kolmogorov-Smirnov, test de Saphiro-Wilks, test de D’ Agostino y test Anderson-Darling. En los test realizados en cada muestra los p-valores obtenidos deberían conducir a una misma decisión sobre la aceptación o rechazo de la normalidad de la variable. Para proceder de forma correcta en el contraste de las dos medias poblacionales por medio de la aplicación de los estadísticos t-student, debería aceptarse la H0 de normalidad de la variable en las dos poblaciones.

La prueba se realiza con al función:

s.mannwhitneyu(col1,col2)

fijándose el valor del nivel de significación igual a 0.05 en la línea 157. La regla de decisión se muestra entre las líneas 156 y 161.

Laboratorio
____________________________________________________________________________________________

• Comparación del caudal de un rio en dos estaciones
  

En un estudio se desea comparar el caudal máximo anual del Rio James (Virginia, EE.UU.) medido en dos épocas diferentes. ¿Qué estadístico utilizaremos? ¿por qué? ¿Qué concluimos en este estudio?

• script:  River.py   
  

• archivo de datos:  River.dat
  

Solución:  ejemplo41.mp4